
Aritmetik Ortalama Nedir? Nerelerde Kullanılır?
Aritmetik ortalama, istatistiksel analiz tablolarında en çok rastladığımız tanımlayıcı istatistik ölçüsü. Tüm araştırmacıların aşina olduğu bu muhteşem ölçüye dair temel kavramları, doğru bilinenleri ve yanlış tabuları bu yazımızda kapsamlıca inceleyeceğiz.
Öncelikle en temel noktalardan başlayalım.
Formül gayet basit: Sayısal bir değişkenin toplamının gözlem sayısına bölümünden oluşuyor. Bu formülü bilmeyen yok.
Peki bu ölçüyü duyduğumuzda ne anlamalıyız? Aritmetik ortalama nedir?
Biz istatistiksel açıdan bakacağız. Aritmetik ortalama, ilgili değişkenimizin genel durumunu temsil eden bir ölçüdür.
Hemen örneklendirelim.
Bir A mahallesinin sosyo-ekononomik durumu üzerine araştırma yapmak istediğimizi düşünelim. A mahallesinin gelirlerinin aritmetik ortalamalası 10.000 TL denildiğinde, o mahallede yaşayanların gelir düzeyinin oldukça iyi olduğunu anlayabiliriz.
Benzer şekilde A mahallesinin gelir ortalaması 1500 TL denildiğinde, o mahalledeki insanların gelir düzeyinin düşük olduğunu hemen algılarız.
Gördüğümüz gibi, verinin merkezi konumunu rahatlıkla görebiliyor; verilerimizin genel durumu hakkında bilgi edinebiliyoruz.
Aritmetik ortalama; sayısal ölçümlerin var olduğu tüm veri setlerinde kullanılabilir, kullanılmalıdır da!
Verilerimizin aralıklı ya da oransal ölçekli olması gerekir.
Kimseye korkutucu gelmesin; bu ölçme türleri, verilerimizin sayısal olması gerektiğini ifade ediyor. Birisi sıfır noktasını yok olarak kabul ederken, diğeri sıfır değerini yok olarak kabul etmiyor.
Hava sıcaklığını düşünelim. Sıfır derece, hava sıcaklığının yok olduğu anlamına gelmez. Ancak gelirimizin sıfır olması, hiç paramızın olmadığı anlamına gelir!
Kısaca sayısal verilerde bu ölçü işimize yarıyor.
Tıptan biyolojiye, fizikten kimyaya, ziraatten eğitim alanına uzanan onlarca uygulamalı çalışmada aritmetik ortalamaya başvurabiliriz.
İstatistiksel analiz uygulamalarında en sık kullandığımız iki alan var:
1) Tanımlayıcı istatistiksel analiz
2) İstatistiksel hipotez testleri
İstatistiksel hipotez testleri özellikle araştırmacılar açısından çok önemli; çünkü araştırmalarımızda hep değişkenler arası ilişkilerin anlamlılığını test ediyoruz. Bu amaçla t-testi, varyans analizi (ANOVA) gibi ortalama karşılaştırma testlerinden yararlanıyoruz.
Hepsinde amaç aynı: ortalamaları karşılaştırmak. Parametrik testlerde aritmetik ortalamaları baz alıyoruz.
Tanımlayıcı istatistiksel analiz aşamasında klasik ortalama ölçüsünü kullandığımız gibi, ağırlıklı ortalamaları da kullanabiliyoruz.
Ağırlıkların toplamı 1’e eşit olacak şekilde her gözleme bir ağırlık ataması yaparak ortalama hesaplayabiliriz. Ağırlıklı ortalamayı da ek bir bilgi olarak not edelim.
Aritmetik Ortalamaya İlişkin Doğrular, Yanlışlar
Bu muhteşem ölçüyü kullanırken yaptığımız çok sayıda yanlışa dikkat çekmemiz gerekiyor.
Önce bir noktayı aydınlatarak başlayalım. Alışkanlıklarımız gereği, ortalama denildiğinde aslında aritmetik olan ortalama ölçüsünü kastediyoruz. Bu artık dilimize oturmuş durumda.
Aslında ortalama, bir verinin merkez noktasını temsil ediyor. Bu temsili medyan da, mod da yapabilir. Bunun için İngilizce’de mean ve average olarak tanımlanmış iki ayrı kavram var.
Bu ayrıma dikkat edelim; kullanırken neyi kastettiğimizin farkında olalım.
Özellikle istatistiksel hipotez testlerini yorumlarken parametrik ve parametrik olmayan testlere göre kastettiğimiz ölçüler değişkenlik gösterir.
Ortalama arası fark vardır dediğimizde parametrik testler için aritmetik ortalama; parametrik olmayan testler için de medyan ya da sıra ortalaması ölçülerini baz almalıyız.
Peki normal dağılmayan veriler için kullanabilir miyiz? Evet, kullanabiliriz. Yeter ki gözlem sayımız 30 ya da 30’dan büyük olsun. Merkezi limit teoremi sayesinde büyük gözlemler için ortalamaların normal dağılıma yakınsadığını biliyoruz.
Normal dağılıma uygun veriler için aritmetik ortalama = medyan = mod eşitliğinin sağlandığına dair bir mit tüm ders kitaplarında yer alıyor. Bu bilgi tamamen teorik düzlemde geçerli.
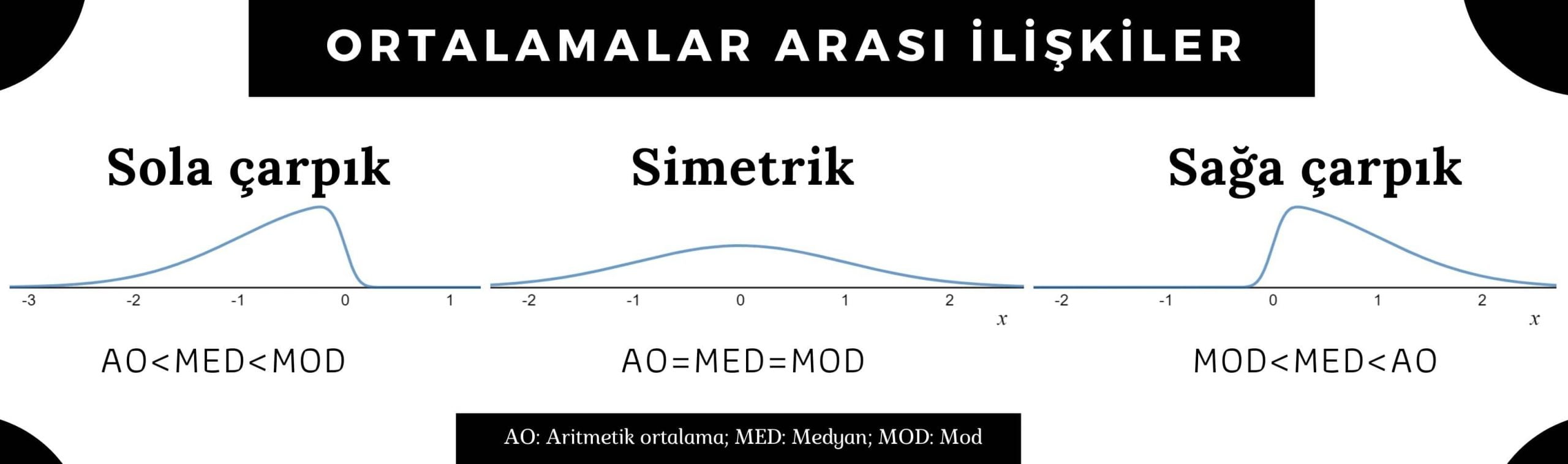
Gerçek hayatta kullandığımız verilerde normal dağılım koşulu sağlansa bile bu eşitlik tam olarak sağlanamıyor. Mutlaka üç nicelik arasında bir farklılık olacaktır.
Verilerimizin çarpıklık durumlarına göre de bu eşitlik değişiyor. Sola çarpık verilerde aritmetik ortalama mod < medyan < aritmetik ortalama sıralaması geçerli iken; sağa çarpık verilerde ise aritmetik ortalama < medyan < mod sıralaması geçerli.
Bir diğer yanlış, sayısal olmayan, yani kategorik değişkenler için kullanılması; bundan da şiddetle kaçınmamız gerekiyor.
Örneğin, kolestrolü 200 olan bir erkek ve 400 olan bir kadının var olduğunu, bu iki kişinin kolestrol ortalamasını hesaplamak istediğimiz düşünelim.
Ortalama kolestol 300 iken, cinsiyet ortalamasını bulabilir miyiz? Elbette hayır. Erkek ve kadının aritmetik ortalaması tabi ki hesaplanamaz.
Adlandırma ölçeğine sahip kategorik değişkenler için en iyisi biz mod ölçüsünü kullanalım.
Peki kategorik verilerimiz sıralayıcı ölçekli; yani doğası gereği bir sıralama içeriyorsa ne yapabiliriz?
Bu durumda da medyan değerini kullanırız. Kaynaklar bize sıralayıcı ölçekli veriler için medyanın daha uygun bir ölçü olduğunu söylüyor. Ama her zaman değil.
Mesela eğitim durumu değişkeni için medyan değerini kullanmak şık olmayacaktır.
Likert tipli bir değişken için 1-5 arası puanların medyan değerini kullanmak son derece uygun olur.
Tekil olarak sıralayıcı ölçekli kategorik verilerin ortalamasını alamasak da; çok sayıda değişkenin aritmetik ortalamasını hesaplayarak skor puanları elde edebiliyoruz.
Bu yaklaşımı özellikle mesleki doyum, sosyal sermaye, yeme bozukluğu gibi kavramsal ifadeleri değelendirmek için kullandığımız anket çalışmalarında kullanıyoruz.
Ölçek geliştirme ve ölçek uyarlama çalışmalarımızda skor puanları oluştururken aritmetik ortalamayı kullanmamızda bir sakınca yok.
Peki verilerimizde aykırı değerler varsa ne yapmalıyız?
A mahallesindeki sosyo-ekonomik araştırmamıza geri dönelim. Ortalama geliri 1500 TL olan A mahallesine aylık geliri 1.000.000 TL olan bir iş adamı eklersek, muhtemelen o mahallenin ortalama geliri de aynı ölçüde yükselir. Ama A mahallesindeki yoksul kişi sayısı değişmez.
Dolayısı ile aritmetik ortalama aykırı değerlere karşı son derece duyarlıdır ve aykırı değerlerin var olduğu durumlarda dayanıklı (robust) ortalama ölçüleri kullanılmalıdır. Bu yanlıştan da kaçınmamız gerekir.
Dayanıklı ortalama ölçüleri için çok sayıda alternatife sahibiz. Medyan, winsorize ortalama, budanmış (trimmed) ortalama, M-tahmincileri gibi çok çeşitli niceliği kullanabiliyoruz.
Bu tür nicelikler, verilerimizdeki aykırı değerlerin etkisini azaltarak genel kitleye ilişkin daha doğru bir ortalama değeri elde etmemizi sağlıyor.
Hesaplamalarımız ve İstatistiksel Analiz Programları
Aritmetik ortalamaları hesaplamak için çok sayıda istatistiksel analiz programına başvurabiliriz.
Hem de bunu kolaylıkla yapabiliyoruz.
SPSS aritmetik ortalamayı Analyze -> Descriptive Statistics ya da Analyze -> Frequency Analysis şeklinde iki adımda hesaplayabilir. R ise mean() fonksiyonu ile elde edebilir. Excel‘de bile tek bir fonksiyon eşliğinde ortalamayı bulabiliyoruz.
Stata‘da Summary statistics menüsünden ortalamaları ve daha birçok niceliği elde edebiliyoruz.
SAS, Minitab, JMP… Tüm istatistik paket programları ve kod tabanlı programlar kolayca aritmetik ortalama hesabını gerçekleştirebilmektedir.
Aritmetik ortalamaları ayrı ayrı değişken bazında hesaplayabildiğimiz gibi, kategorik değişkenlerin grupları bazında da hesaplayabiliyoruz. İstatistiksel karşılaştırmalarımız için ortalamaların hesaplanması bize müthiş yorumlama kolaylığı sağlıyor.
SPSS bu işlemi t-testi ve ANOVA testinin içerisinde kendiliğinden bize sunuyor. İstatistiksel çıktılarda tanımlayıcı istatistik şeklinde ortalamaları bulabiliyoruz.
Minitab programında ANOVA menüsünden varyans analizi hesaplarken de grup bazında aritmetik ortalamalar veriliyor. R’nin içerisinde de compareGroups gibi paketlerde ortalamaları doğrudan alabiliyoruz.
Özetle bu yazımızda aritmetik ortalama kavramına dair hem teknik, hem de pratik bilgiler sunmaya çalıştık. Sıkça tekrarladığımız bazı hatalarımızdan nasıl kaçınacağımızı açıkladık. Bazı doğruları da tekrar tekrar vurguladık.
Matematiğin bizlere sunduğu bu basit ama olağanüstü ölçü sayesinde değişkenlerimizin doğası, genel durumu hakkında kolaylıkla bilgi edinebiliyoruz. Yeter ki aritmetik ortalamanın kıymetini bilelim, onu doğru yer de, doğru şekilde kullanalım.