
Çoklu Regresyon Analizi SPSS Programında Hangi Adımlarla Uygulanır?
Regresyon analizi istatistiksel analiz uygulamalarında bağımlı değişkenimizi modellemek için kullanılmaktadır. Bağımsız değişken sayımız birden fazla ise çoklu regresyon analizini tercih ediyoruz. Çoklu regresyon analizi SPSS programı ile kolaylıkla uygulanabiliyor.
Bu yazımızda çoklu regresyon analizinin SPSS programı ile nasıl uygulanacağını ve nasıl sonuçlar alacağımızı konuşacağız.
Öncelikle SPSS yazılımı bağlamında regresyon analizinden bahsedelim.
Her ne kadar regresyon analizi sanki tek bir modelmiş gibi düşünülse de, istatistik biliminde çok sayıda farklı regresyon modeli bulunmaktadır. Tüm bu modellerin bir yapısı Genelleştirilmiş Lineer Modeller (GLM) olarak tanımlanıyor.
GLM, apayrı bir yazı konusu diyelim ve devam edelim.
Ancak araştırmalarda bu modelleri yokmuşçasına yalnızca normal lineer regresyon modelleri varmış gibi hareket ediyoruz.
SPSS ile Regresyon Analizleri
SPSS’nin seçeneklerinde normal, Poisson, gama, negatif binom ve lojistik regresyon gibi alternatif modeller bulunuyor; önce bunu ortaya koyalım.
Hangi regresyon modelini kullanırsak kullanalım, bağımsız değişken sayısına göre iki tür regresyon analizi tanımlanıyor:
1) Basit regresyon analizi : Tek bir bağımsız değişken kullanılır.
2) Çoklu regresyon analizi: En az iki bağımsız değişken kullanılır.
Bağımlı değişkenimizin normal dağılıma uygun olduğu varsayımı altında, çoklu regresyon analizi SPSS programı ile üç adıma basitçe uygulanabilir. SPSS’ye ait adımlar şu şekildedir:
Analyze -> Regression -> Linear
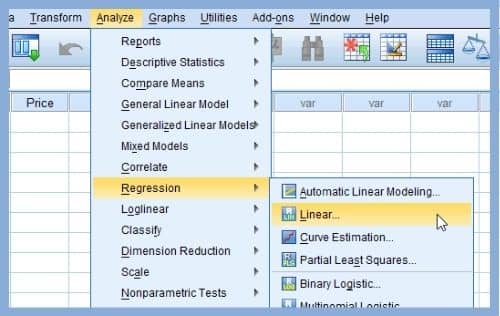
Yukarıdaki şekilde de gördüğümüz gibi adımlar oldukça basit. Linear seçeneğini işaretlediğimizde, baştan normal dağılıma uygun bağımlı değişkenimizi modellemek istediğimizi kabul ediyoruz.
Linear seçeneğini tıkladığımızda, karşımıza aşağıdaki ekran çıkıyor.
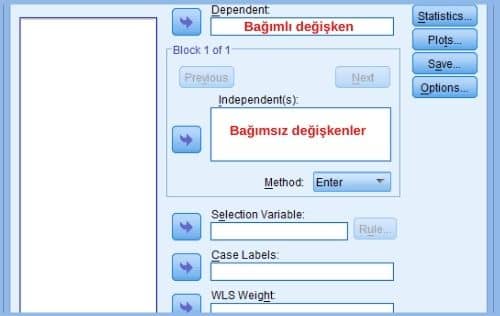
Karşımıza açılan ekranda en önemli iki bölüm Dependent ve Independent(s) bölümleri.
Dependent=Bağımlı değişkenimizi tanımladığımız alan. Burada yalnızca tek bir bağımlı değişken tanımlayabiliyoruz.
Independent(s)=Bağımsız değişken(ler)imizi tanımladığımız alan. Buradan bir ya da birden çok bağımsız değişken tanımlayabiliriz. Çoklu regresyon analizinden bahsettiğimiz için çoğul tabiri kullanabiliriz.
Sol bölümde daha önceden SPSS’ye eklediğimiz değişkenleri sol tarafa sürükleyerek bırakmamız yeterli.
Bağımlı değişken bölümüne atadığımız değişken mutlaka ama mutlaka sayısal olmalı.
Kategorik bir değişkeni bağımlı değişken bölümüne tanımlamamlıyız!
Bağımsız değişkenlerimiz ise kategorik de olabilir; sayısal da. Bu noktada bir sınırlamamız yok.
Ancak SPSS programında değişkenlerimizin türlerine dikkat etmemiz şart. String türündeki değişkenlerimizi bu bölümlere atayamıyoruz. Numeric türündeki değişkenleri tercih etmemiz en doğrusu.
SPSS ile Regresyon İstatistklerinin Seçimi
Çoklu regresyon analizi SPSS programı ile uygulanırken, regresyon modelimize özgü yapabileceğimiz çok sayıda farklı seçenek bulunuyor. Pencerimizde bulunan Statistics seçeneğini tıkladığımızda aşağıdaki pencere karşımıza çıkıyor.
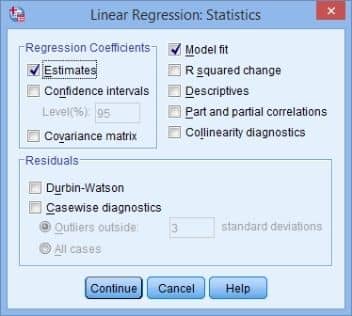
Açılan pencerede normal lineer regresyon analizine ilişkin istatistik seçenekleri çıkıyor.
Bu seçeneklerde nelerin yer aldığına kısaca göz atalım.
Estimates seçeneği regresyon katsayılarını, yani istatistik dilindeki beta katsayılarını veriyor. Bu sayede bağımsız değişkenlerimizin bağımlı değişken üzerindeki lineer etkisini matematiksel olarak görebiliyoruz.
Confidence intervals seçeneği de beta katsayılarımıza ait güven aralıklarını gösteriyor. Salt güven aralıklarına baksak bile, beta katsayılarımızın istatistiksel olarak anlamlı olup olmadığını tespit edebiliyoruz.
Güven aralıklarımızın hangi güven düzeyinde hesaplanacağına da karar verebiliyoruz. SPSS programının kendi hazır değeri %95 olarak veriliyor.
Confidence intervals seçeneği beta katsayılarımıza ait varyans-kovaryans matrisini bize sunuyor. Nasıl ki değişkenlerin varyans-kovaryans matrisleri varsa, parametre tahminlerimizin de varyans-kovaryans matrisleri var.
Model fit seçeneği regresyon analizi sonuçlarımızda ANOVA tablosunu, çoklu korelasyon katsayısını, belirtme katsayısını (R-kare) ve modelin standart hatasının tahmin değerini bize sunuyor. Bu açıdan olmazsa olmazsa adımlardan birini oluşturuyor.
R squared change seçeneği modelimize yeni bir değişkenin eklenmesi sonucunda R-kare değerimizin nasıl değişeceğini gösteriyor. Bu adım modele yeni bir değişkeni eklediğimizde anlamlı bir katkının oluşup oluşmayacağını bize gösteren spesifik bir seçim işleminden oluşuyor.
Descriptives seçeneği değişkenlere yönelik tanımlayıcı istatistikleri bize gösteriyor. Tanımlayıcı istatistiklerden aritmetik ortalama ve standart sapma değerlerini görebiliyoruz. Ayrıca bu seçenek bize değişkenlerimize dönük Pearson korelasyon analizi sonuçlarını matris şeklinde sunuyor.
Part and partial correlations seçeneği bize bağımsız değişkenlerimize yönelik sıfır-dereceli, kısım ve kısmi korelasyonları ayrı ayrı veriyor.
Collinearity diagnostics seçeneği bize çoklu bağlantı probleminin tespitine yönelik varyans şişirme faktörü (VIF) ve koşul indeksi gibi istatistikleri sunuyor. Bu istatistiklerden yola çıkılarak, çoklu regresyon analizi SPSS uygulamalarında çoklu bağlantı probleminin ortaya çıkıp çıkmadığına ilişkin fikir yürütebiliyoruz.
Çoklu regresyon analizi SPSS programı ile uygulanırken artık değerlerimiz, yani hatalarımıza dair birtakım özel istatistikleri Residuals bölümünden elde edebiliyoruz. Şimdi bu seçeneklere göz atalım.
Durbin-Watson seçeneğinde hata değerlerinden hareketle otokorelasyon probleminin olup olmadığını test edebiliyoruz. Bu seçenek bize Durbin-Watson testinin sonuçlarını sunuyor.
Casewise diagnostics seçeneği bize hata değerlerimize yönelik istatistikleri sunuyor. Bu bölümden hata paylarında aykırı değerin olup olmadığını belirleyebiliyoruz. Outliers outside şeklinde görülen rakama göre, hangi gözlemlerin aykırı değer sınıfına girebileceğini kendimiz tanımlayabiliyoruz.
Çoklu regresyon analizi SPSS programı ile modellenirken, burada yer alan değer 3 standart sapma olarak belirlenmiş. Buna göre hata değeri 3 standart sapmadan uzak olan hatalar potansiyel aykırı değer olarak belirleniyor ve çıktılarda varsa bize gösteriliyor.
Ayrıca bu bölümde yer alan istatistiklere göre hatalara ait ortalama, standart sapma, minimum ve maksimum değerlerini de gözlemleyebiliyoruz. Bu değerler bize modelimizin varsayımlarını (örneğin hata ortalaması sıfır olup olmadığını) kontrol etmemizi sağlıyor.
Çoklu regresyon analizi SPSS ile uygulanırken Save seçeneğinden bir takım özel ölçümleri (Cook uzaklığı, standardize artıklar vb.) kaydedebiliyoruz.
Ayrıca Plots seçeneğinden de regresyon sonuçlarımıza dair bir takım istatistiksel grafikleri de çizdirebiliyoruz. Bu grafikler ve kaydedilen değerler sayesinde modelimizin genel sonuçlarını, varsayımsal bulguları ve gözlemlerimizin potansiyel sorunlarını belirleyebiliyoruz.
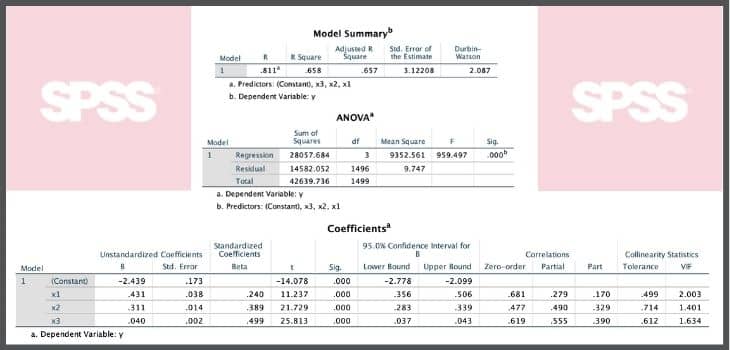
Yukarıdaki şekilde üç bağımsız değişkenden oluşan çoklu regresyon analizi sonuçlarını görebiliyoruz. Burada model özeti, varyans analizi (ANOVA) tablosu ve regresyon katsayılarına ilişkin istatistik tablosunu görmekteyiz.
SPSS çıktısında belirtme katsayılarını, modelimizin F-istatistiklerini, beta katsayılarımızı (ham ve standardize), t-istatistiklerimizi, katsayılara ait güven aralıklarını (%95 güven düzeyinde), anlamlılık değerlerini ve çeşitli korelasyon ölçülerini gözlemleyebiliyoruz.
Yukarıda sunulan SPSS çıktısında istatistiksel olarak anlamlı sonuçların yer aldığı bir çoklu regresyon modeli yer alıyor. Model istatistiklerinde belirtme katsayısı, ANOVA tablosu, regresyon katsayılarının anlamlılık testleri gibi çok sayıda bulgu var.
Çoklu Regresyon Analizi SPSS Uygulamalarına Yönelik Son Söz
Elbette şu ana kadar detaylandıramadığımız konular da var. Söz konusu seçeneklerimizi hep Enter metoduna göre anlattık. Burada farklı metotlar, farklı ağırlıklandırmalar, farklı seçme işlemleri gibi alternatif konular da bulunuyor.
Ayrıca bu seçeneklerin işaretlenmesi sonucunda oluşan çıktıların yorumlanması da başlı başına bir makale çalışmasını hak ediyor. Şimdilik bu yazıda çoklu regresyon analizi SPSS uygulamalarına yönelik en kilit unsurları tanımladık.
Sizleri istatistik analiz bilgileri ile boğmak yerine, çoklu regresyon analizi SPSS programında uygulanırken karşımıza nelerin çıkabileceğini göstermek istedik.
Son tahlilde; çoklu regresyon analizi SPSS programında nasıl uygulanır sorusuna yanıt aramaya çalıştık. Eksik kalan bölümleri de gelecek yazılarımızda tamamlamaya çalışacağız.