
Mahalanobis Uzaklığı ve Aykırı Değer Tespiti
Aykırı değer, istatistiksel analiz uygulamalarında sıkça karşımıza çıkan bir olgudur. Araştırma verilerimizde aşırı ölçüm değerleri içeren aykırı değerlerin tespit edilmesi de son derece önemlidir. Mahalanobis uzaklığı, aykırı değerlerin tespit edilmesi için kullanılan istatistiksel yaklaşımlardan birisidir.
Öncelikle aykırı değer tespiti ile ilgili kısaca bir bilgilendirme ile başlayalım.
Veri setlerimiz tek bir değişken veya çok sayıda değişken içerebilir. Tek değişkenli verilerimizde aykırı değer tespiti yapabilmek için z-skorlarını kullanabiliriz. Ancak çok değişkenli veri setlerimizde ilgili gözlemin aykırı değer olup olmadığını belirlemek için alternatif yaklaşımlar gerekiyor.
Elbette aykırı değer analizi için verilerimizin sayısal ölçümler içerdiğini varsayıyoruz.
Çünkü kategorik veriler için klasik Mahalanobis uzaklığını doğrudan uygulayabilmek teorik açıdan kesinlikle yanlış. Bunun için geliştirilen özel ölçülere başvurmak gerekiyor.
Çok değişkenli veriler için aykırı değerin olup olmadığını nasıl anlayabiliriz? İlk aklımıza gelen gözlemlerin genel ortalamadan ne ölçüde saptıklarını gözlemlemek olacaktır. Ama tam bu noktada çok dikkatli davranmak gerekiyor.
Gözlemlerin ham ortalamalarının yanı sıra, standart sapmalarını da göz önüne almamız gerekiyor. Yani ortalamadan aşırı ölçüde farklılaşma durumunun, standart sapmaya kıyasla ne ölçüde gerçekleştiğini de dikkate alarak aykırı değer tespitine yönelmeliyiz.
İşte tam bu amacımız doğrultusunda kullanacağımız mükemmel bir uzaklık ölçüsü var: Mahalanobis uzaklığı.
Adı üstünde, bir uzaklık ölçüsünü kullanıyoruz. Bu uzaklık, gözlemlerin ortalamadan sapmalarını ölçümlemek için kullanılıyor. Söz konusu uzaklığı kullanırken değişkenlerin kovaryans matrisleri de dahil ediliyor.
Bu meşhur uzaklık ölçüsü, ünlü Hintli istatistikçi Prasanta Chandra Mahalanobis tarafından geliştirilmiş.
Formülasyonu da oldukça basit. X çok değişkenli bir veri setini, μ ise ortalama vektörünü ve Σ kovaryans matrisini temsil ettiğinde, D(X, μ) şeklindeki Mahalanobis uzaklığı şu şekilde gösteriliyor:
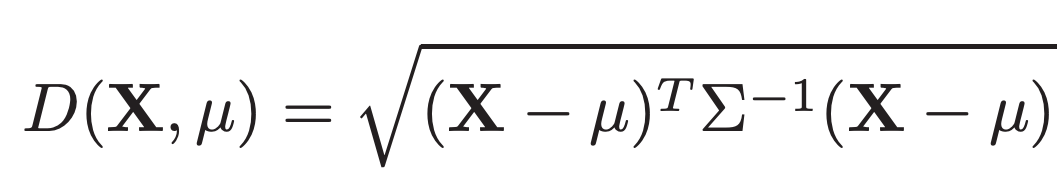
Bu uzaklık değerleri verilerimizin çok değişkenli normal dağılıma uygunluğu varsayımı altında, ki-kare dağılımına uygunluk gösteriyor. Korelasyonsuz değişkenler için de Öklid uzaklığına denk geliyor.
Diyelim Mahalanobis uzaklıklarını hesapladık. Bu durumda gözlem sayımız kadar bir uzaklık ölçüsü hesaplamış oluyoruz. Peki bu uzaklıklara göre aykırı değerleri nasıl tespit ediyoruz?
Yanıtı son derece basit. Bu uzaklıklar ki-kare dağılımına uyduğu için, değişken sayımızı serbestlik derecesi alarak ki-kare tablo değerimizi belli bir hata payı ile hesaplıyoruz. Yani tablo değerimizden sayısal olarak büyük olan uzaklığa sahip gözlemler, aykırı değer olarak belirleniyor.
Bunun için de belirlediğimiz bir hata payına göre (genelde %1 veya %5) tablo değerine bakıyoruz.
Mahalanobis uzaklığını gözlem bazında hesaplayabilmemiz için R-Project en elverişli istatistiksel analiz programı. Ancak regresyon analizi kapsamında SPSS ile de Mahalanobis uzaklığını hesaplayabiliyoruz.
Ayrıca Python, Matlab vb. analiz yazılımları ile kod yazarak bu uzaklıkları hesaplayabiliriz.
R-Project’in bu noktada sunduğu en büyük avantaj, Mahalanobis uzaklığının hesaplanmasında sağladığı esnekliktir. Bu noktada farklı kovaryans matrisleri veya merkezi konum ölçülerini entegre edebiliyoruz.
Mahalanobis uzaklığı kendi içerisinde çok sayıda farklı konu barındırıyor. Hangi kovaryans matrisi seçilmeli? Çok değişkenli normallik varsayımınının aykırı değer belirleme performansı üzerine etkisi var mı? Hata payı aykırı değer tespiti için önemli mi? Yüksek boyutlu verilerde Mahalanobis uzaklığı nasıl hesaplanmalı?
Tüm bu sorular, ayrı bir makale konusunu hak ediyor. Gelecek yazılarımızda Mahalanobis uzaklığını daha derinlemesine inceleyeceğiz.