
Yüksek Standart Sapma Normal Dağılımı Etkiler mi?
İstatistiksel analiz sürecinde sayısal verilerimize dair bilinen bir tabuyu sorgulayalım: standart sapma normal dağılım sonucu üzerinde kesin bir etkiye sahip midir? Bu sorunun cevabını somut örnekler üzerinden inceleyeceğiz. Öncelikle standart sapmanın verilerimizin yayılımı üzerindeki etkisini inceleyelim.
Araştırma verilerimizde zaman zaman ortalamaya kıyasla yüksek standart sapma değerlerinin elde edildiğini gözlemlemekteyiz. Hatta çoğu zaman böyle bir sonuçtan kaçınmak isteriz. Ancak veriler üzerinde bir manipülasyon (yani hile) yapmadıkça bu sonuçtan kaçınamayız.
Dolayısı ile bilimsel doğruluktan şaşmamak adına gerçek standart sapma sonuçlarını vermek zorundayız.
Elbette yüksek standart sapma, verilerin ortalama etrafında büyük saçılmalar gösterdiğine işaret eder ve bu durumun gerçekleşmesini istemeyiz. Özellikle ortalamaya çok yakın ya da ortalamadan yüksek bir standart sapma, verilerin son derece heterojen dağıldığına işaret etmektedir.
Bu durum her ne kadar istenmese bile, araştırmamızda bir hata veya yanlışlığın var olduğunun kesin göstergesi olamaz.
Peki sayısal olarak büyük standart sapma normal dağılım sonuçlarını etkileyebilir mi? Cevap: Hem evet, hem hayır. Yani bazı durumlarda verilerimizin standart sapmasının yüksek olması normal dağılıma uygunluğun sağlanamadığını gösterebilir; ama her zaman bu durum geçerli değildir.
Bu durumu sayısal veriler düzleminde örneklendirelim.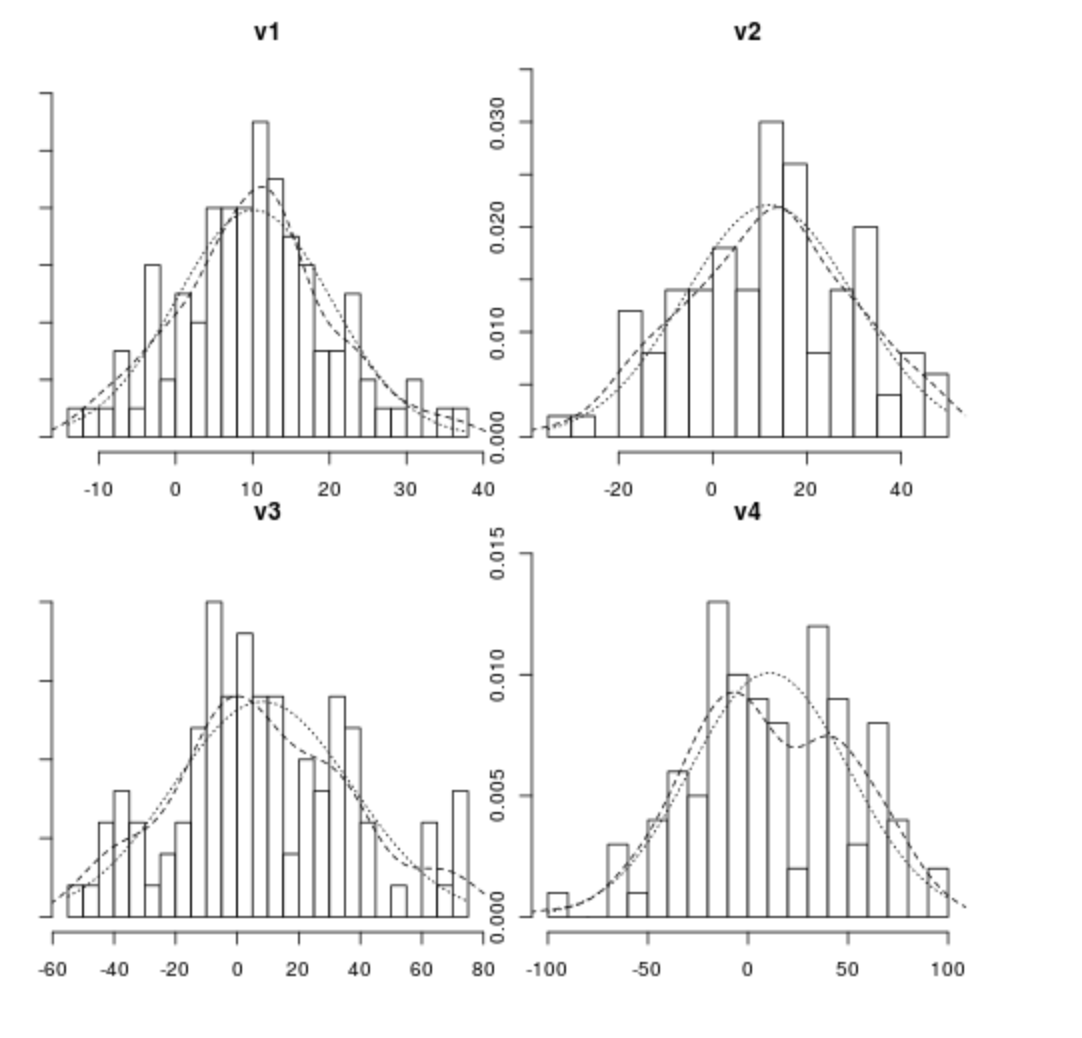
Yukarıdaki şekilde n=100 gözleme sahip v1, v2, v3, v4 şeklinde gösterilen dört ayrı değişken bulunmaktadır. Buradaki değişkenlerin tümünün aritmetik ortalamaları 10’dur ve standart sapmaları da ortalamanın sırasıyla 1, 2, 3 ve 4 katı olacak şekilde hesaplanmıştır. Sırayla tanımlayacak olursak:
- v1: Aritmetik ortalaması 10 ve standart sapması 10 olan bir değişken
- v2: Aritmetik ortalaması 10 ve standart sapması 20 olan bir değişken
- v3: Aritmetik ortalaması 10 ve standart sapması 30 olan bir değişken
- v4: Aritmetik ortalaması 10 ve standart sapması 40 olan bir değişken
Bu veriler ışığında histogramlara bakıldığında her bir değişkenin normal dağılıma uygun olduğu çok net bir şekilde görülmektedir. Ayrıca bu veriler için uyguladığımız Shapiro-Wilk normallik testi sonucunda normal dağılım koşulunun sağlandığı da tespit edilmiştir (p>0.05).
Dikkat edilirse standart sapmaların ortalama göre büyük ölçüde yüksek olduğu durumlarda bile normallik durumlarında bir bozulma meydana gelmemektedir. Standart sapma ortalamaya kıyasla 4 kat büyük olduğunda bile verilerimiz hala normal dağılıma uygundur.
Bu durumun tam aksi de gözlenebilmektedir. Örneğin verilerimizde olası bir aykırı değerin bulunması durumunda, standart sapma çok yüksek değerlere erişebilir ve söz konusu aykırılık verileri normal dağılımdan uzaklaştırabilir.
Sonuç olarak istatistiksel veri analizi süreçlerinde ezber bilgilere değil, bilimsel deneylere güvenelim ve yüksek standart sapma normal dağılıma uygunluğu engeller görüşünün her zaman geçerli olmadığını unutmayalım.