Korelasyon analizi, istatistik analiz süreçlerimizde değişkenlerimiz arasındaki ilişkileri araştırmak için kullanılan eşsiz bir yöntem. Korelasyon katsayısı hesaplamalarımız ile araştırma değişkenlerimiz arasındaki ilişkilerin anlamlılığını, yönlerini (her zaman değil) ve derecesini inceliyoruz.
Korelasyon Katsayısı ve Merak Edilenler
Bu yazımızda korelasyon katsayılarına dair ıskalanan bazı önemli olguları 10 maddede sorgulayacağız.
Korelasyon katsayılarına yönelik bilgilerimizi Genel Bilgiler ve Nicel Değişkenler için bilgiler olarak iki bölüme ayırdık.
Korelasyon Katsayısına Yönelik Genel Bilgiler
Önce hem nicel, hem de kategorik değişkenlere yönelik olgular ile başlayalım.
Korelasyon katsayısı yalnızca nicel verilerin tekelinde değildir! Nicel-nicel ve kategorik-kategorik nicel-kategorik değişken çiftleri için de hesaplanabilir.
Korelasyon analizinden konu açıldığı anda aklımıza ilk gelen verilerin nicel olduğu ve normal dağılımının varsayımının sağlandığı durumlarda başvurduğumuz Pearson korelasyon ölçüsü.
Halbuki biz hem iki kategorik, hem bir nicel bir kategorik, hem de iki kategorik değişken için korelasyon katsayısı hesaplayabiliyoruz.
Burada dikkat edilmesi gereken en temel hususların başında da değişkenlerin ölçme düzeyleri geliyor. Özellikle kategorik verilerin ölçme düzeylerine göre özel katsayılar var.
Örnek olarak aşağıdaki katsayıları verebiliriz:
- Phi katsayısı
- Cramer katsayısı
- Sakoda katsayısı
- Eta katsayısı
- Hellinger korelasyon katsayısı
- Pearson-m katsayısı
- Kontenjans katsayısı
- Polikorik korelasyon katsayısı
Bazı ölçüleri hiç duymamış olanlar olabilir. Bunun en büyük sebeplerinden birisi de SPSS=İstatistik denkleminin bizde yarattığı korkunç yanılgı. Burada var olan istatistikler dışındaki kavramlardan pek haberdar değiliz.
Korelasyon katsayısının yorumlanabilmesi için istatistiksel olarak anlamlı olması gerekir.
Korelasyon analizi sonucunda elde ettiğimiz katsayıyı yorumlayabilmemiz için iki değişken arasında istatistiksel olarak anlamlı bir ilişkinin var olması zorunludur.
Aksi halde ilişkisi anlamlı olmayan iki değişken hakkında ne söyleyebiliriz?
Bunu şöyle düşünelim.
Birisi size “Amerika Birleşik Devletleri Başkanı ile ilişkiniz nasıl , iyi mi?” diye sorduğunda (çok büyük bir çevreniz ya da torpiliniz olmadığı sürece) %99’umuz karşımızdakinin akıl sağlığı ile ile ilgili kuşkuya kapılır.
Çünkü çoğumuzun Donald Trump ile anlamlı bir ilişkimiz yok!
Dolayısı ile ilişkinin gücünü, iyi ya da kötü olmadığını söyleyemeyiz.
Aynı şey istatistik biliminde de geçerli: Anlamsız ilişkiler yorumlanamaz.
Ancak anlamlılık da korelasyon analizi için ayrı bir problem konusu. Kimi zaman 0.301 olarak hesaplanan katsayı istatistiksel olarak anlamlı bulunurken; 0.502 olarak hesaplanan katsayısı anlamsız çıkabilir.
Bu durum gözlem sayısına ve seçilen korelasyon katsayısına göre değişebilir.
Korelasyon katsayısı her zaman [-1,1] aralığında değildir.
Pearson korelasyon analizi sonucunda evet; elde ettiğimiz katsayı [-1,1] aralığında yer alıyor. Ama diğer korelasyon katsayıları için bu durum geçerli değil.
Kategorik veriler için hesapladığımız katsayılar farklı değer aralıklarında yer alabiliyor.
Örneğin; Phi katsayısının üst sınırı 1 değildir. Maksimum ilişki seviyesinde bile, çapraz tablolara göre 0.7 civarı değerler alabilir.
En sık kullandığımız Spearman’ın katsayısı 1’den büyük değerlere sahip olabilir!
Sakoda katsayısı [0,1] aralığında yer alır.
Dolayısı ile bu çarpık algıyı da düzeltmemiz gerekiyor.
Korelasyon katsayısı için güven aralıkları da dikkate alınmalıdır.
Hesapladığımız katsayıların alt ve üst sınırlarının hesaplanması bize geleceğe dönük çok yararlı çıkarımlar sunabilir. Katsayımızın üst sınırının ulaşacağı değere göre ilişkinin ne boyutlara erişeceğini kestirebiliriz. Benzer şekilde katsayımızın alt sınırı da ilişkin ne ölçüde zayıflayabileceğiniz bize gösterir.
Hemen bir örnek verelim.
Düzenli maske takmama ile korona virüse yakalanma durumları arasındaki ilişkinin r=0.55 düzeyinde olduğunu düşünelim. Eğer bu katsayımızın güven aralıklarına göre üst sınır değeri 0.95’e ulaşırsa, düzenli maske takmama ile korona virüse yakalanma olgusunun yüksek ölçüde ilişkili olabileceğini düşünebiliriz.
Korelasyon katsayıları çok değişkenli istatistiksel analizler içerisinde de kullanılır.
Korelasyon katsayıları bir araya gelir ve korelasyon matrislerini oluştururlar.
Korelasyon matrislerini de temel bileşenler analizi, açıklayıcı faktör analizi, doğrulayıcı faktör analizi gibi tekniklerde de kullanıyoruz. Bu açıdan da çok değişkenli istatistiksel veri analizi süreçlerinde korelasyon katsayıları çok önemlidir.
Ayrıca regresyon analizi gibi modelleme teknikleri kapsamında çoklu bağlantı sorununun tespiti gibi farklı amaçlar için de kullanabiliyoruz.
Nicel Değişken Çiftleri İçin Korelasyon Katsayısına Yönelik Temel Bilgiler
Korelasyon analizinin en sık kullanıldığı veri setleri nicel değişkenlerden oluşmaktadır. Şimdi nicel değişkenler için bazı olgulara göz atalım.
Korelasyon katsayısı nicel veriler için monoton ilişkiler var olduğu durumlar için kullanılabilir.
Monoton ilişki ne demek? Düzenli olarak ya artma, ya da azalma eğiliminde olan; yani belli bölgelerde ters yönlü, belli bölgelerde aynı yönlü ilişkinin olmadığı durumları kastediyoruz.
Kısacası, nicel veriler arasında non-lineer ilişkilerin var olduğu durumlar için korelasyon katsayısını kullanılmaz.
Korelasyon katsayısı iki nicel değişkenden birisinin tüm değerleri aynı ise hesaplanamaz.
Bazı veri setlerimizde değişkenimizin ölçüm değerleri tüm gözlemler için aynı olabilir.
Örneğin anketimizde çocuk sayısını sorduk ve tüm katılımcılar 2 seçeneğini işaretlediler. Çocuk sayısı ile vücut kitle indeksi arasındaki ilişkiyi değerlendirmek istersek; çocuk sayısı hiç değişmediği için hesaplayamayız.
Özetle standart sapması 0 olan değişkenlerin var olduğu durumlarda, nicel veriler arası korelasyon katsayısı hesaplanamaz. Bu sonucu R, SPSS gibi istatistik yazılımlarında da görebiliriz. Bu yüzden hata alırsanız şaşırmayın!
Korelasyon katsayısı seçilirken değişkenlerin dağılımları da göz önüne alınmalıdır.
Nicel değişkenler için korelasyon analizi uygularken, normal dağılım varsayımın karşılanıp karşılanmamasına göre Pearson, Spearman ya da farklı bir korelasyon ölçüsünü kullanabiliriz. Ancak gözlem sayımızın yüksek olduğu durumlarda merkezi limit teoreminden hareketle normallik varsayımı ihlal edilse bile parametrik katsayılardan yararlanabiliriz.
Gözlem sayımız düşük ve normallik varsayımı ihlal edilmiş ise, bu durumda parametrik olmayan yöntemlere (Spearman, Kendall vb.) başvurmamız kaçınılmazdır.
Aykırı değerlerin var olduğu durumlarda klasik korelasyon katsayıları kullanılamaz.
Eğer nicel verilerimiz aşırı büyük ya da küçük değerler içeriyorsa, ya da verilerimizin içerisinde farklı bir dağılım mekanizmasından türetilen gözlem kümeleri varsa; kısaca aykırı değer varsa, klasik korelasyon katsayılarından şiddetle uzak durmamız gerekiyor!
Peki neden?
Nedeni oldukça basit. Çünkü bu aykırı değerler katsayının olması gereken değerden büyük ölçüde sapmasına yol açabilir. Pozitif ilişki varken negatif Pearson korelasyon katsayısı ile karşılaşabilmemiz mümkün!
Aykırı değer varsa, bu durumda dayanıklı (robust) korelasyon katsayılarına müracaat etmemiz gerekiyor. Bu da bizi farklı istatistik programlarına mecburen yöneltebilir, çünkü SPSS, Minitab gibi yazılımlarda dayanıklı korelasyon analizi seçeneği yok.
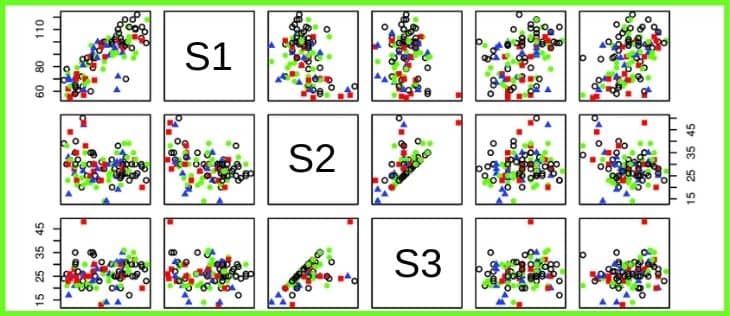
Korelasyon katsayısı nicel değişkenler için incelenirken serpilme diyagramının incelenmesi gerekir.
Korelasyon katsayılarımızı hesaplamadan önce nicel değişkenler arası ilişkileri gözlemlemek ve olası aykırı değerleri inceleyebilmemiz için önce serpilme diyagramını incelememiz gerekiyor.
Konu başlıklarında incelediğimiz olguların bir kısmını serpilme diyagramları üzerinden değerlendirebiliyoruz.
Örneğin nicel değişkenlerimiz arasında monoton bir ilişkinin var olup olmadığını serpilme diyagramı sayesinde kontrol edebiliriz. Değişkenlerimiz arasındaki ilişkinin ters yönlü ya da aynı yönlü olduğunu yine serpilme diyagramı sayesinde belirleyebiliriz.
Ayrıca verilerimizde olası bir aykırı değerin varlığını da yine serpilme diyagramı sayesinde gözlemleyebiliriz.
Kısacası değişkenlerimiz için korelasyon katsayısını hesaplamadan önce serpilme diyagramının incelemesini şiddetle öneriyoruz.
Kategorik veriler için de elde edilebilen harika veri görselleştirme araçları bulunuyor. Bu araçlar aracılığı ile de çok sayıda çıkarım yapabiliyoruz.
Korelasyon katsayılarına dair sonsöz
Bu yazımızda korelasyon katsayılarına dair bilmemiz gereken 10 farklı olgu üzerinde durduk, tartıştık. Kuşkusuz istatistik analiz uygulamalarına ihtiyaç duyan herkes için korelasyon analizi çok önemli.
Araştırmacıların korelasyon katsayılarına dair ifade ettiğimiz bu 10 temel konuyu dikkate alarak, bilimsel açıdan mükemmel korelasyon analizleri gerçekleştirmesini diliyoruz!
